Convolution, Circulant Matrices, and Eigenanalysis
Convolution
Perhaps the most ubiquitous operation in digital signal processing is the application of filters on signals via convolution. The convolution operation is defined as:
\[y[n] =(h * x)[n] = \sum_{m=0}^{N-1} h[n-m] x[m]\]where $x[n]$ is the input signal with entries $(x_0, …, x_{P-1})$, $h[n]$ is the filter with entries $(h_0, …, h_{L-1})$, $y[n]$ is the output with entries $(y_0, …, y_{N=P+L-1})$.
Properties:
- Linearity:
- Commutativity:
Delta Function and Shifts
An interesting function is the delta function which is defined as:
\[\delta[n] = \begin{cases} 1, & \text{if } n = 0,\\ 0, & \text{if } n \neq 0 \end{cases}\]The delta function has an identity property under convolution:
\[x[n] = x[n] * \delta[n]\]Similarly a shifted delta function yields a shifted copy of the input sequence:
\[x[n - m] = x[n] * \delta[n - m]\]Any finite sequence $x[n]$ of length $P$ can be represented as a weighted sum (linear combination) of shifted delta functions
\[x[n] = \sum_{m=0}^{P-1} x_m \delta[n - m]\]In fact, shifted delta functions serve as the basis vectors in time domain, and this is equivalent to a $P \times P$ identity matrix. Recall a vector can be expressed as a linear combination of the columns of a matrix $A$ where the columns of $A$ are the basis vectors for that space: \(v = \sum_n c_n A_{:, n}\)
Circular Convolution
A related operation is circular convolution:
\[y[n] = x[n] \circledast_N h[n] = \sum_{m=0}^{N-1} h[(n-m)\text{ mod } N] x[m]\]Circular Convolution can be used to compute regular convolution (sometimes called linear convolution) if $x$ and $h$ are padded with zeros such that the new lengths equal $P + L - 1$, and the output truncated to the length of $P+L-1$.
Example:
- $\delta[n - 1] \circledast_P x[n]$ yields a circularly shifted sequence by one entry: $(x_{P-1}, x_0, …, x_{P-2})$
Fourier Transform
The Discrete Fourier Transform (DFT) of a signal $x[n]$ of length $N$ is defined as [1] :
Analysis:
\[X[k] = \frac{1}{\sqrt{N}} \sum_{n = 0}^{N-1} x[n] W_N^{kn}\]Synthesis:
\[x[n] = \frac{1}{\sqrt{N}} \sum_{n = 0}^{N-1} X[k] {W_N^*}^{kn}\]where $W_N = e^{-j\frac{2\pi}{N}}$, $W_N^* = e^{j\frac{2\pi}{N}}$, and $0 \le k \le N-1$
The analysis portion of the DFT can be seen as a matrix muplication:
\[X[0] = \frac{1}{\sqrt{N}}(x[0] + x[1] + x[2]... + x[N-1])\] \[X[1] = \frac{1}{\sqrt{N}}(x[0] + x[1]W_N + x[2]W_N^2... + x[N-1]W_N^{N-1})\] \[\vdots\] \[X[N-1] = \frac{1}{\sqrt{N}}(x[0] + x[1]W_N^{N-1} +x[2]W_N^{2(N-1)} + ... x[N-1]W_N^{(N-1)(N-1)})\]which is equivalent to
\[\begin{bmatrix} X[0] \\ X[1] \\ \vdots \\ X[N-1] \end{bmatrix} = \frac{1}{\sqrt{N}} \begin{bmatrix} 1 & 1 & 1 & ... & 1 \\ 1 & W_N & W_N^2 & ... & W_N^{N-1} \\ \vdots & \vdots & \vdots & ... & \vdots \\ 1 & W_N^{N-1} & W_N^{2(N-1)} & ... & W_N^{(N-1)(N-1)} \end{bmatrix} \begin{bmatrix} x[0] \\ x[1] \\ x[2] \\ \vdots \\ x[N-1] \end{bmatrix}\] \[X = Fx\]where $F$ is the Discrete Fourier Transform Matrix. The synthesis formula can be similarly written as a matrix multiplication:
\[\begin{bmatrix} x[0] \\ x[1] \\ \vdots \\ x[N-1] \end{bmatrix} = \frac{1}{\sqrt{N}} \begin{bmatrix} 1 & 1 & 1 & ... & 1 \\ 1 & W_N^* & {W_N^*}^2 & ... & {W_N^*}^{N-1} \\ \vdots & \vdots & \vdots & ... & \vdots \\ 1 & {W_N^*}^{N-1} & {W_N^*}^{2(N-1)} & ... & {W_N^*}^{(N-1)(N-1)} \end{bmatrix} \begin{bmatrix} X[0] \\ X[1] \\ \vdots \\ X[N-1] \end{bmatrix}\] \[x = F^*X\]Note how $F^* = F^\texttt{H}$ and $I = F^*F = FF^*$, this is because the DFT matrix is an unitary matrix. From the synthesis formulation above, one can see that the Fourier coefficients can be interpeted as coordinates with the columns as the basis vectors. The basis vectors consist of various sinusoidal forms. The basis set consists of a set of $N$ functions enumerated by $k$ of the form $\omega_k[n]= e^{j\frac{2\pi}{N}kn}$ for $n=0,…,N-1$ [3 , 5] . Below are pictured the Fourier basis vectors for $N = 16$
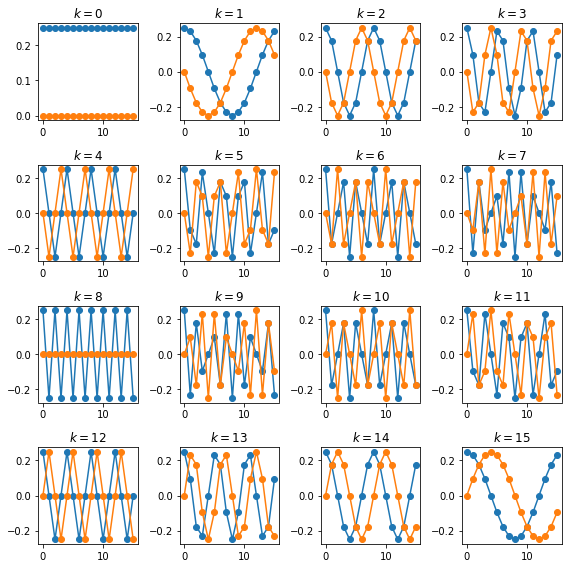
DFT and Circular Convolution
DFT can be used apply circular convolution:
\[Y[k] = \frac{1}{\sqrt{N}} \sum_{n = 0}^{N-1} y[n] W_N^{kn}= \frac{1}{\sqrt{N}} \sum_{n = 0}^{N-1} (x[n] \circledast_N h[n]) W_N^{kn}\] \[Y[k] = \frac{1}{\sqrt{N}} \sum_{n = 0}^{N-1} y[n] W_N^{kn}= \frac{1}{\sqrt{N}} \sum_{n = 0}^{N-1} W_N^{kn} \sum_{m=0}^{N-1} h[n-m \text{ mod } N] x[m]\] \[\frac{1}{\sqrt{N}} \sum_{n = 0}^{N-1} y[n] W_N^{kn}= \frac{1}{\sqrt{N}} \sum_{m=0}^{N-1} \sum_{n = 0}^{N-1} W_N^{kn}h[n-m \text{ mod } N] x[m]\]Since the DFT of $h[n-m]$ equals $W_N^{km}H[k]$
\[=\sum_{m=0}^{N-1} H[k] x[m] W_N^{km}\] \[Y[k] = \sqrt{N}H[k]X[k]\]Convolution reduces to element-wise multiplication in the Fourier domain.
Circulant Matrices
The entries in circulant matrices follow this pattern:
\[H_{n,m} = h[{(n-m) \text { mod } L} ]\]where $h \in \mathbb{R}^L$.
\[H = \begin{bmatrix} h_{0} & h_{L-1} & \cdots & h_{1} \\ h_{1} & h_{0} & \cdots & h_{2} \\ \vdots & & \ddots & \vdots\\ h_{L-1}& h_{L-2} & \cdots & h_{0} \end{bmatrix}\]Circulant Matrices and Convolution
If $H$ is circulant and $x \in \mathbb{R}^L$ then the entries of $y=Hx$ are given by:
\[y_n = \sum_{m = 0}^{L-1} H_{n,m} x_m\] \[y_n = \sum_{m=0}^{L-1} h_{(n-m) \text { mod } L}x_m\]Thus, circular convolution can be expressed as matrix multiplication with a circulant matrix.
Circulant Matrices and the DFT
First let’s inspect the eigenvectors $f$ and eigenvalues $\lambda$ of the circulant matrix:
\[Hf = \lambda f\]The $n \text{ th }$ entry of $f$ is given by:
\[f_n \lambda = \sum_{m = 0}^{L-1} h_{(n-m) \text { mod } L}f_m\] \[f_n \lambda = \sum_{m = 0}^{n} h_{n - m} f_m + \sum_{m = n+1}^{L-1}h_{L-m+n}f_m\]$n-m=q$ and $L-m+n=q'$ and commutativity of addition
\[f_n \lambda =\sum_{q = 0}^{n} h_{q} f_{n-q} + \sum_{q' = n+1}^{L-1}h_{q'}f_{L+n-q'}\]If $f_k = \frac{1}{\sqrt{L}}\rho^k$
\[\frac{1}{\sqrt{L}} \rho ^n \lambda =\sum_{q = 0}^{n} h_{q} \frac{1}{\sqrt{L}}\rho^{n-q} + \sum_{q' = n+1}^{L-1}h_{q'}\frac{1}{\sqrt{L}}\rho^{L+n-q'}\] \[\lambda =\sum_{q = 0}^{n} h_{q} \rho^{-q} + \sum_{q' = n+1}^{L-1}h_{q'}\rho^{L-q'}\]If $\rho^{L} = 1$
\[\lambda =\sum_{q = 0}^{n} h_{q} \rho^{-q} + \sum_{q' = n+1}^{L-1}h_{q'}\rho^{-q'}\] \[\lambda =\sum_{q = 0}^{L-1}h_{q}\rho^{-q}\]Note the condition $\rho^{L} = 1$ can satisfied by $\rho_v = \exp{j2\pi v/L}$ for $v = 0, …, L-1$. In fact, this is how we extract all of the $L$ eigenvalues of $H$:
\[\lambda_v =\sum_{n = 0}^{L-1}h_{n}e^{-j2\pi vn/L}\]along with the corresponding eigenvector $f_v[n] = \frac{1}{\sqrt{L}}\exp{(j2\pi vn/L)}$. Note how the eigenvalues correspond to the Fourier transform values of $h[n]$ scaled by $\sqrt{L}$. This proof was a modified version of the proof found in [4].
The eigendecomposition of $H$ is given by:
\[H = F^*\Lambda F\]where $F$ is a Discrete Fourier Transform matrix from earlier. If we apply $H$ to an input signal $x$
\[y = Hx = F^*\Lambda F x = F^*\Lambda X = F^*(\text{diag}(\Lambda) \circ X)\]Recall $X$ is the Fourier Transform of $x$, $\text{diag}$ extracts the diagonal of a matrix, and $\circ$ is the Hadamard product. $\text{diag}(\Lambda) \circ X$ matches the formula of $Y[k] = \sqrt{L}H[k]X[k]$. For further reading see [2].
References:
- Oppenheim, Alan V., John R. Buck, and Ronald W. Schafer. Discrete-time signal processing. Vol. 2. Upper Saddle River, NJ: Prentice Hall, 2001.
- Michael Bronstein, Deriving convolution from first principles, July 2020
- Jonathan Goodman, Fourier and von Neumann analysis, 2016
- Gray, Robert M. Toeplitz and circulant matrices: A review. Now Publishers inc, 2006.
- M. Lustig. Lecture Notes from EE16B Designing Information Devices and Systems II